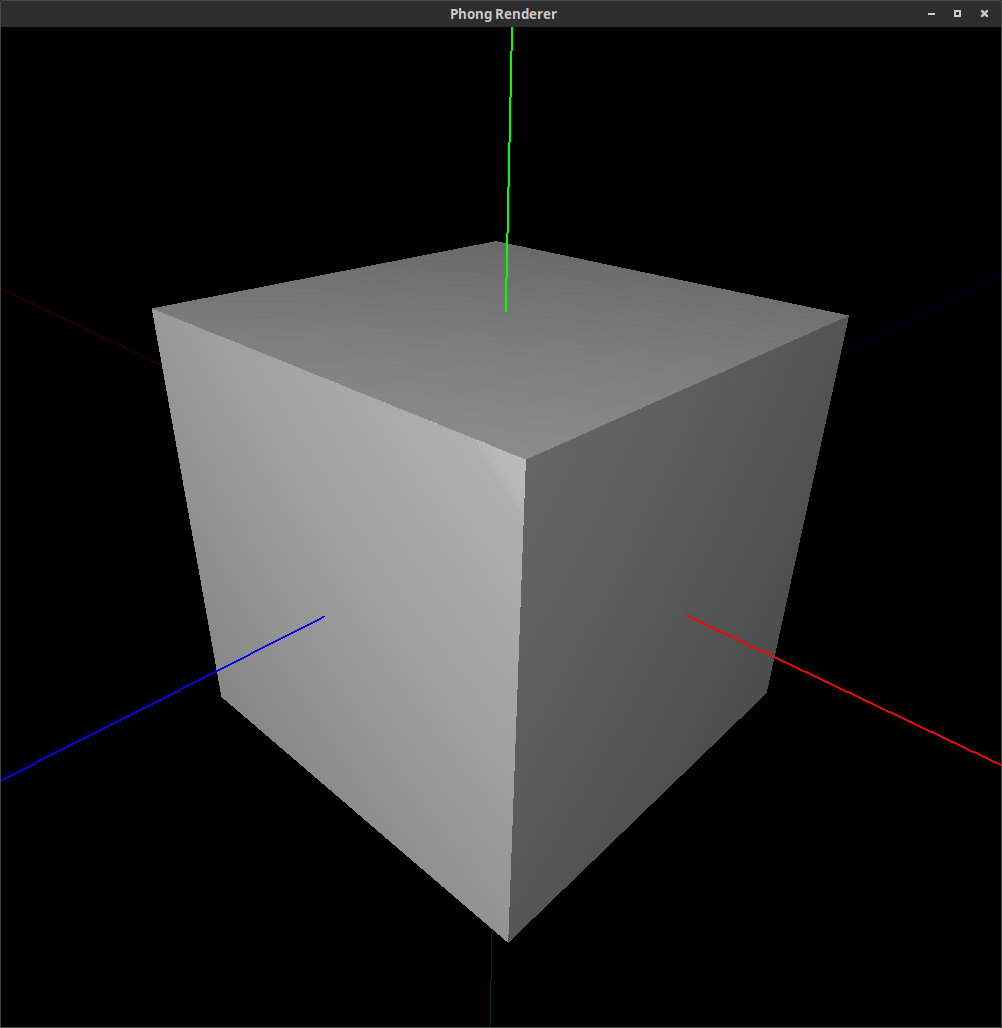
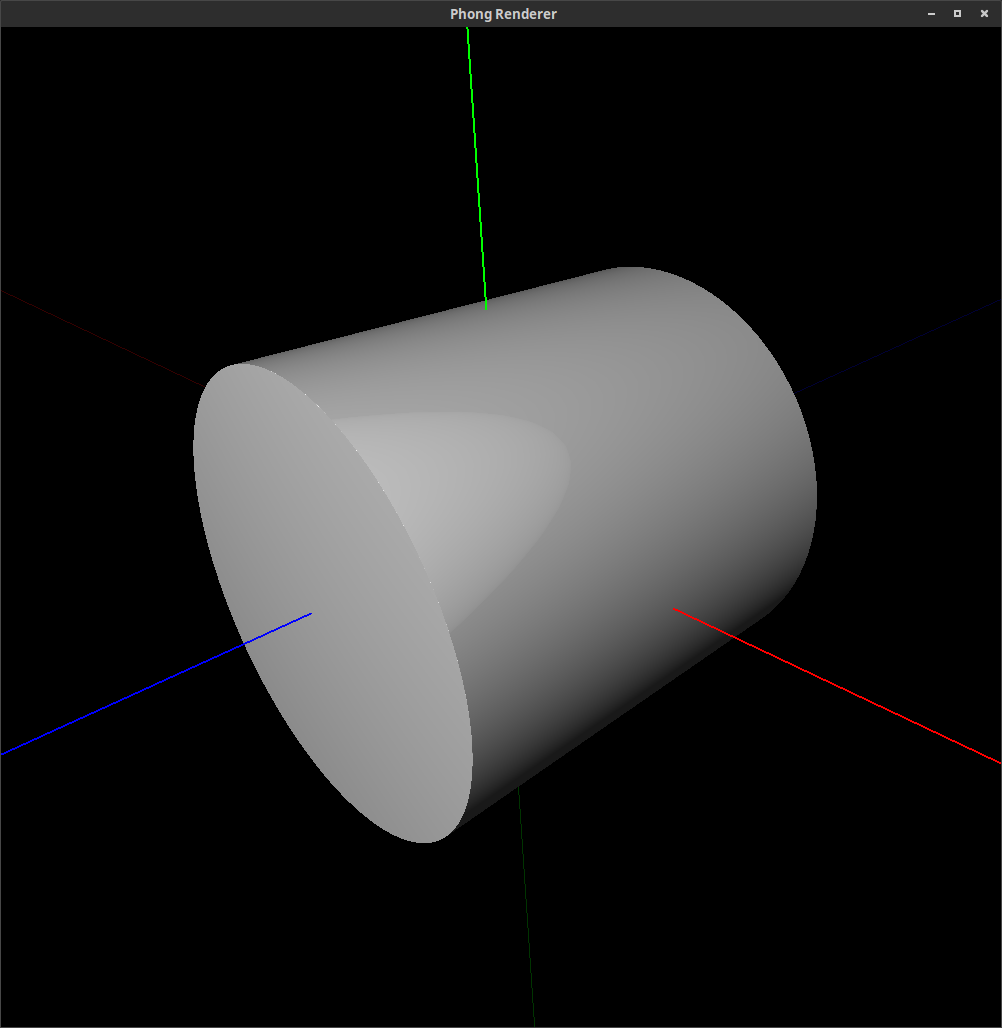
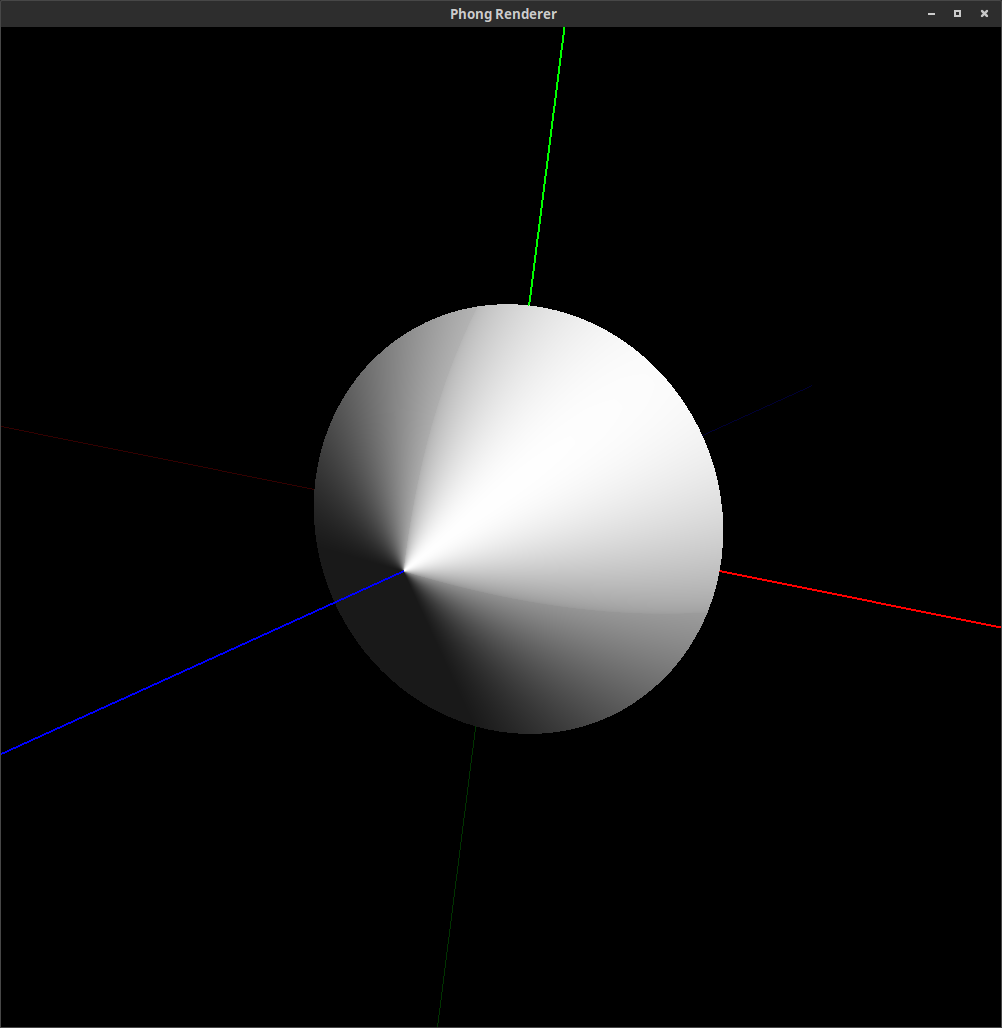
Figure 1:
Assignment 7 Lecture Notes
The following will act as lecture notes to help you review the material from lecture for the assignment. You can click on the links below to get directed to the appropriate section.
Superquadrics are a family of inside-outside functions (defined below) which allow us to generate a variety of implicit three-dimensional shapes that we can easily compute normals and gradients for; perfect for a simple raytracing program to work with.
In order to define the shapes we’ll be ray tracing, we use an inside-outside function, defined to be some such that
Many common solids can be defined this way, such as the unit cube, unit sphere, octahedron, unit cylinder, and double cone:
One can see that by setting the left-hand side of side of these equations to 0, we get an implicit
definition for each of these shapes.
Instead of having to use a variety of different functions for different shapes however, we introduce superquadrics, which themeselves are a three-dimensional generalization made by Prof. Barr in 1981, of Lamé curves (also known as Piet Hein’s “superellipses”). The general superquadric function can then be defined to mimic the surfaces described above, amongst others. It is even possible to extend the math to create toroids; however, we limit the scope to dealing solely with ellipsoids, defined by a longitudinal shape parameter and latitudinal parameter .
Thus, we get the general inside-outside function of superquadrics as:
Looking at the general form, we can verify that when this become the same inside-outside function as the unit sphere, and similarly, when , we have an octahedron.
Keep in mind that when computing the result of this function, the squaring of the , and values must occur prior to the other exponentiation since negative coordinates would cause computational errors.
With an implicit definition of a particular superquadric, we can also compute the surface normal at a given point by computing the gradient of the superquadric function. We therefore have:
The following images are rendered images of superquadric surfaces. (They were actually rendered with the command line and rendering tool that you will be using in Assignment 7.) By varying the longitudinal and latitudinal parameters, , and respectively, we can create the shapes shown below.



Figure 1:
1.5 Transforming Implicit Functions
So far, we’ve only considered superquadrics centered at the origin, but in order to make scenes, we want to be able to position our objects arbitrarily.
Specifically, given some scalar inside-outside function (little) of point little , we want to know how to find the resulting scalar function (big) as a function of the point, big .
How can we make something that serves as an inside-outside function for the same surface under some transformation that takes one point to another, i.e., which takes (little) to (big) ?
As an example, let’s consider the 3D point transformation given by
where , , and are some translation, rotation, and scaling operations respectively. Then, we have the inverse transformation as
We can then plug this into the relation between our original and transformed inside-outside functions to get an expression for (big) .
Thus, in order to calculate the inside-outside function of a transformed superquadric, you must first apply the inverse transformation to the position vector or point in question, and feed this into the original untransformed function.
Keep in mind that when using this technique to make sure that you are clear on what space you are in when you compute different things.
For example, if you had a point that you want to find the surface normal for on some inside-outside function under some transformation , then you should transform the point to the point , compute the normal vector for using (little) in body coordinates, and then transform the resulting normal back by applying a version of for normals: don’t forget that transformations work differently for normal vectors than points, and you’ll also have to normalize these normal vectors, so they’d have magnitude 1.
For (forward) transforming normal vectors, you use the inverse transpose of the 3x3 matrix part of the transform. (See the Assignment 2 lecture notes if you need a refresher).
On the same note, if you have a directional vector such as the direction for the ray, (perhaps if you parameterized a point to be an origin plus a directional vector times ), in order to compute an inside-outside function with transformation properly, the origin point of the ray needs to be transformed as stated above with the inverse transformation matrix of .
But the direction for the ray, should be transformed with the inverse transformation matrix without translations in order to preserve the correct resulting point that corresponds to adding the two. Alternatively, you could compute the actual point by adding the directional vector to the origin prior to doing any transformation and transform the point as stated above.
In order to understand what we mean by “a ray for each pixel,” I find that it helps to imagine putting a wire screen, as you might find on a window, some distance in front of your face. You’d still be able to tell what’s behind it, but your view would be divided up into a grid.
If you then chose a point in each square of the grid and colored the entire square to match that point, then you’d end up with a similar-looking image, relative to what you were actually seeing, without the screen.
If the squares were large, it might look highly “pixelated” like an old videogame, but as you increased their density you’d get a sharper image.
This is essentially how scenes are represented on computer screens: we can’t represent the light from the (by definition) infinite number of points, so we sample them at regular intervals and call it good enough. To ray trace an image, we think about the actual grid of pixels on the monitor as being the wire screen from before, and send a ray out from our camera through a point in each pixel in order to fill it in with a color.
Now that we know how to express the surface of a superquadric and compute its normal vectors, how do we follow light from the camera back to the surface of objects? For simple contours such as planes we can solve for the intersection between a vector and the surface explicitly, but for superquadrics we must use an iterative solver to produce an estimation. One such technique that produces accurate results but is still fairly straightforward is that of Newton’s method.
Many of you will recall from calculus that a Taylor series is a method of approximating the function around the point , given by
If we ignore the higher order terms as they are comparatively small in the neighborhood of , then we can say that if , we have
This tells us that if we’re at some point and want to get to another point where is a root of , then we can approximate using , , and .
This can be made into an iterative process by replacing with and with , so that if we start from some initial value of , we can compute our next approximation of as
and then plug this again in as to get another approximation of , and so on and so forth until we hit some “stopping condition.” We label this value as , and take it to be that . As you may have guessed, we will be using the superquadric function () and its derivative for and , since finding the intersection of a vector and a superquadric’s surface is the same as finding where along the vector we will have .
It is of course possible that , which would cause divide-by-zero errors at runtime - you should check for this.
So what do we use as our initial value of ? A simple way to bound superquadrics is to use a sphere larger than the largest unit superquadric, which is a cube. The radius of the bounding sphere must therefore be , which in turn gives us an inside-outside function for it:
Now, we know we can express the equation of a 3D line parallel to the 3D vector that passes through the 3D point as
Where varies across . If we let the point be the location of our camera, then we can solve for the intersection of a ray exiting the camera and the bounding sphere of a superquadric by solving
This is just a quadratic equation in with coefficients where
so then we can solve for .
But before you do this, note that this ray, , needs to be first transformed into the body coordinate system, from world coordinates, before it can be plugged into the above bounding sphere equation! The above sphere equation is in its body coordinates at the origin.
We could use the standard quadratic formula to solve this equation,
but this has numerical problems when is small, relative to , so we would be subtracting two values that are very close to each other, losing many bits of precision.
Numerically Improved Version of the Quadratic Equation Solutions. You can create a numerically improved quadratic equation solver by never canceling the square root term with the term, so these can always add.
When , and is small relative to , a numerical problem takes place with the “plus” term in front of the square root term, i.e., for , where and the square root are almost the same magnitude, canceling and losing many bits of precision.
This problem doesn’t take place with the “minus” sign in front of the square root term. So one of the above algebraic solutions is numerically “bad” and the other is “good.”
To derive a better expression, you can multiply numerator and denominator by to cancel out many terms in the original numerator, initially where is smaller than .
So when the two solutions to select are:
When you’ll never be canceling out a square root term that has the opposite sign from the term in the solution, so you will not be losing as much accuracy with these versions of the solutions.
Now, to handle the case when you can multiply both sides of the quadratic equation by which is , so you can get a new quadratic equation that never has a negative value, since .
Just don’t multiply both sides of the equation by zero! There is a similar function, which is zero when . Don’t use that similar function!
The above equation is equivalent to our original equation, where we’ve multiplied both sides of the equation by a nonzero number, , which is .
There are two roots for the new quadratic equation, which we will call and . If we care which root is which, if then and . If then and . This can most easily be seen in the final expression for which is the same as the conventional quadratic equation formula, but with an extra factor on the square root, reversing its sign when .
This is an “improved” version for the two numerical solutions of the quadratic equation. The term never cancels with the square root, since both items have the same plus or minus sign.
And then the expressions were further simplified, for the final expressions to use for and .
Both for negative and non-negative values of , these final expressions numerically work for values of , , and for the original quadratic equation; you can algebraically test the two roots of the new final expressions of and to see that they are still valid, surprisingly, even when is or is not smaller than !
And again note that the value of must never be zero! It should be +1 or -1.
In computer graphics, the improved numerical values for can remove jagged artifacts in ray tracing at the silhouette boundaries of shapes like spheres, when the quadratic equation needs to be solved. (Oops, our bounding spheres will usually not need the extra accuracy.)
The above cases were covered, because in computer graphics, it can be important to know how to solve the quadratic equation correctly!
Next, there are two more things to consider. The first is that our discriminant may be negative, leading to imaginary values of . This corresponds with cases where the ray misses the bounding sphere entirely, so you should check for this and handle it accordingly.
The second is that we have two solutions for , and . The physical interpretation of this fact is intuitive, as a ray may intersect a sphere in at most two locations. If both values of are positive, then starting point is outside the sphere and the smaller value is on the side of the sphere closer to the camera, and thus closer to the ray’s actual intersection with the superquadric. In this case, your initial guess should be .
If one value is positive and the other negative, then is inside the sphere, and the ray may or may not hit the superquadric while traveling away from the eye. In this case, both and could be tested as initial guesses. If either produces a positive solution for through the Newton’s method solver, then the trick is to know whether the ray intersects the superquadric on the way in or the way out. If one solution is positive and one is negative, then we know is inside the superquadric, and the outside surface can’t be seen. If both are positive, however, then we know the ray goes in one side and comes out the other. If both are negative, then the superquadric is entirely behind the camera, and can’t be seen.
As with the Newton’s method solutions in the previous case, we know that if both and are negative, then the bounding sphere is behind the camera and thus invisible, since the ray has to travel backwards to hit it.
Note that for the assignment, using when it is positive should be sufficient for the scenes we provide.
Between floating point math and the inherent approximation made by our Newton’s method solver, we can’t simply iterate until we find a value of such that . Instead, we can stop when the value of a superquadric’s inside-outside function is close enough to zero. A good approximation of this is when we are within one twentieth or so of a pixel’s width away from the actual surface, but the gist is that must be sufficiently close to 0.
However, we can also take advantage of the fact that we know some information about As long as we are approaching the superquadric along a ray, the inside-outside function should be positive and decreasing, and thus should be negative. If ever it becomes positive, then traveling further along the ray should take us farther away from the superquadric. Thus, if the sign of ever changes from to , we know we’ve missed the superquadric.
Additionally, on the surface of a superquadric we will have , so if this is ever the case we should also check if . If this is satisfied as well, then we know we’re on the superquadric’s surface already, and can just use our current value for without computing . On the other hand, if and is nowhere near 0, the math is effectively the same as the sign change case mentioned above.
Above all else, remember that is the position of the camera, is the direction the camera is looking, so
describes a ray leaving the camera.
To “plug” it into the scalar inside outside function , however, we need to transform the ray into the local coordinate system first. The matrix transforms of a straight ray are still a straight ray. So we need to use the body coordinate system version of the ray, using vector in body coordinates and the body coordinate system version of the point .
So
is the function to use in Newton’s method as it tests whether the ray is inside a superquadric, and
is its derivative.
Now that we know what to do, the question is how to do it: how do we express each ray in the form , so that we can use our Newton’s method solver? This is actually just a poorly-disguised exercise in linear algebra.
First, we define the screen to be the front plane of the camera frustum. In this class so far, you’ve likely only dealt with frustums given by their near, far, left, right, top, and bottom components, but our program uses another common representation based on the near and far components, along with the camera’s vertical field-of-view (FOV) and aspect ratio. The FOV is defined to be the angle between the vector from the camera to the horizontal midpoint of the top of the screen and the vector from the camera to the horizontal midpoint of the bottom of the screen, while the aspect ratio is simply the x-resolution divided by the y-resolution.
From this, we can easily calculate the height and width of the front plane of the frustum, assuming that the camera is centered within it. If its distance from the camera (i.e. the near component) is , the FOV is , and the height of the plane is , then from basic trigonometry we know that
where is the unique angle in an isosceles triangle of height and base . If the aspect ratio is then , and the width of the plane is , we have
Once we have and , we can divide the plane up into an by grid.
Now we need to find the vector from the camera through each point on the grid, which can easily be done by finding the vector which would translate us from the camera’s position to that point.
We begin by defining three basis vectors, , , and . is simply the direction the camera is looking, which is before the camera rotation is applied. We then take to be the one pointing directly to the right relative to the camera, which is initially , and to be the one pointing directly upwards relative to the camera, which is initially .
Adding to the camera’s position takes us to the exact center of the screen. If we then translated again by we’d be at the midpoint of the right edge of the screen, and then another translation by would take us to the top right corner. From this, it should make sense that adding or subtracting takes us right or left by a pixel, while adding or subtracting takes us up or down by a pixel.
This is really all we need. If we define to be , with being an integer in , and to be , with being an integer in , then pixel can be expressed as , where is the position of the camera. You can verify that this produces sane results by plugging in , which should take us to the bottom left corner, or , which should take us to the top right. Note that for the purposes of this derivation, I have defined the -axis to be increasing along the upwards direction, which is the opposite of graphics convention.
Now we recall that our rays should be expressed in the form . It doesn’t really matter how long is, since whatever value of we solve for will be correct for the given . Thus, we can simply take , with taking us to a point on the front plane of the frustum.
2.4 Lighting Model and Shadows
As you should have demonstrated in your intersection test from part a, we can find the normal at any point on the surface of a superquadric. Because the Phong model calculates lighting at any point on a surface given the normal, we can easily reuse it here to figure out the color at a ray-superquadric intersection.
However, ray tracing allows us to incorporate further complexities into the Phong model, the simplest of which is shadowing. Let us define an object to be illuminated by a point light as long as the path from the light to the object is unobstructed. At each point we apply the Phong model to, we can check each light to see if it’s obstructed by sending a ray out from the light to the intersection point (or vice-versa) and testing whether it hits any other superquadrics before hitting the one we initially intersected with. If the intersection point is and the position of the light is , then is given as , and when we’ve reached the intersection point. You must do this in your lighting calculations.
Other more advanced capabilities when using raytracing to render images include handling reflections and refractions, but will not be in the scope for this class. You could imagine that given we implemented all these different extensions, the rendered images become very realistic and life-like since we are effectively modelling light as we see it in our physical world.
Original written by Parker Won and Nailen Matschke (Class of 2017).
Modified and adapted by Lokbondo (Loko) Kung (Class of 2018). Also Al Barr,
2020.
Links: Home