CS11 Erlang - Lab 2

Sieve of Eratosthenes, Process-Style

The Sieve of Eratosthenes is a simple way of generating prime numbers. The basic idea is this:

Generate a list of numbers from 2 to some maximum value N.
Starting with the first number in the list (that is, 2):
1. The current number is prime.
2. Remove from the list all multiples of the current number.
3. Move forward to the next number that still remains in the list.
4. Go back to step (a).

So for example, if you had the list:

  [2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25]

Starting with the number 2, you know that 2 is prime from the above rules, and you remove all multiples of 2. You end up with a list like this:
```
  [_2_, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25]
```
Move forward in the list to the next number, which is 3. By the above rules, 3 is prime, and you remove all multiples of 3. This gives you the list:
```
  [2, _3_, 5, 7, 11, 13, 17, 19, 23, 25]
```
Then you move forward to the next number, which is 5. You know that 5 is prime, and you remove all multiples of 5, giving the list:
```
  [2, 3, _5_, 7, 11, 13, 17, 19, 23]
```
And so forth...

This is the general idea.

Specification

We are going to implement the Sieve of Eratosthenes, but with a twist! Instead of using a list of numbers, we will use a series of Erlang processes that function as sieves, and the messages will be the numbers. As numbers flow through the sequence of processes, you will end up with only prime numbers at the end.

Create a new Erlang module called "proc_sieve". This module should export a single function called "generate", which takes a single argument "MaxN", and returns a list of all prime numbers between 2 and MaxN, inclusive.
The generate function will first spawn a "sieve" process (described below), and then send this sieve process each number from 2 to MaxN in sequence. Each integer is sent as a separate message to the sieve process. Finally, when all integers have been sent, the generator will send a final message to its sieve process, but we will get to that in a moment.
The "sieve" process should be implemented with a function that takes no arguments, because all of its information will be passed via messages. The sieve process follows a relatively simple set of rules:
- The first thing the sieve process does is to receive and store an integer. This number, called N, is prime.
- From this point forward, the sieve process receives more messages, which are either integers, or a special "done" message. The basic idea is that the sieve will filter out all incoming numbers which are multiples of N, only passing on the numbers that are not multiples of N.
Subsequent incoming messages are handled like this:
- If the incoming message is a number, and the number is a multiple of N, the sieve just ignores the message and goes on to the next message. That is, the sieve filters out the multiple of N. (Use the rem integer-remainder operation to compute this.)
- The first time that the sieve encounters a number that is NOT a multiple of N, the sieve process needs to start a new sieve process in the chain. Let's call this number P. We know that P is prime, because it is the first non-multiple of N that this sieve process has seen. Therefore, this sieve should start a new sieve process, send the new process P as its first message (thus setting the new sieve's prime number N to be P), and then from that point on, this sieve sends its filtered results on to the next sieve.
  
  Note: Do not start the next sieve-process until you actually need it, because otherwise it will sit there and never go away. You need to make sure that your program doesn't leak processes.
- Finally, the sieve process handles one other message as well, and this is of the form {done, ReqPid}. This message tells the sieve process that the computation is finished, and it's time to collect all the prime numbers back to the generator. The sender of this message includes its PID as well, so that the sieve process can send the entire list of primes from that point all the way to the end of the process-chain, back to the requester.
  
  If this sieve process is the last sieve in the chain, then its job is very simple. All it has to do is to send its value of N back to the requester, as a list. (In other words, the code will be something like this: ReqPid ! [N].)
  
  However, if the sieve process is NOT at the end of the chain, then it needs to send its own {done, self()} message to the next sieve, get back the list of results, prepend its own value of N, and then send the full list back on to its requester.
  
  As you can see, this will cause the "done" message to propagate all the way down the entire chain of sieve processes, and then the list of prime numbers will be accumulated from the very last sieve process, all the way back to the first one in the list.
You can see from all of these details, that each sieve process will have two pieces of state: the sieve's value of N, which doesn't change throughout the lifetime of the process; and also the PID of the next sieve in the chain, if a "next sieve" has actually been created. You could, for example, use the atom undefined to represent the situation where the "next sieve" has not yet been created, and once a "next sieve" has been created, you can store the sieve's PID for that state value instead.
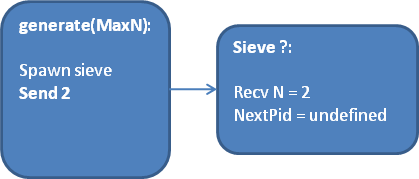
Now that you see how the sieve processes work, you can see that the last thing that the generate function must do is to send a {done, self()} message to the first sieve process, and then receive the list of prime numbers from the first sieve process.

Sketch of Operation

This is a pretty complicated procedure to describe in words, so here are some simple sketches to illustrate what is going on. When the generator starts up, it spawns a single sieve process for filtering out all numbers that are multiples of 2:

Once the sieve process receives N = 2, its job is to filter out all multiples of 2. However, the first non-multiple of 2 that it sees is a new prime number, which we call P. Therefore, the sieve must start its own child-sieve and then send P on to the child:

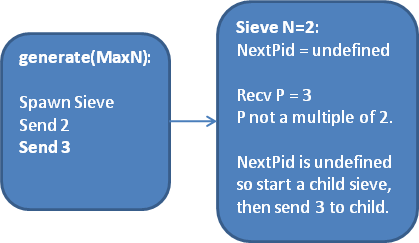
The next value received from the generator is 4, and the N=2 sieve will filter out that value:

Of course, when the generator sends a value of 5, this passes through both the N=2 sieve and the N=3 sieve, because 5 is also prime. Thus, the N=3 sieve must now start a child sieve:

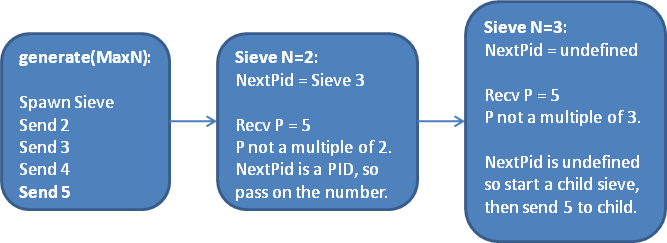
And so forth, until after running for quite a while, we end up with a situation like this:

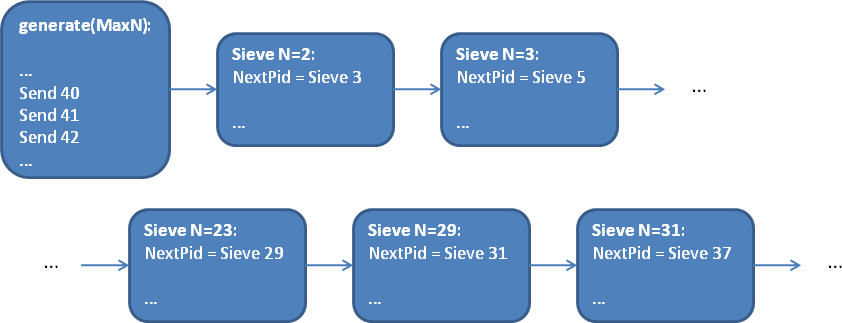
At the end, of course, the generator needs to send its {done, self()} message to the first sieve in the chain, and then this "done" message propagates all the way to the end of the chain of processes. Finally, the last sieve in the chain receives the "done" message, and the actual prime numbers are collected from the end back to the start.

Testing and Printing Primes

Once you have completed your prime number generator, you need to test it to make sure it works properly. You probably want to start with a simple test, like MaxN = 100, just to make sure that it works correctly.

Make sure that your generator doesn't leak any processes! All sieve processes should terminate successfully at the end of a run, and it should be possible to run "generate" multiple times without any adverse behaviors. You can find out how your solution behaves by running the processes/0 BIF before running your code, and then again after running your code, to see if there are suddenly lots of extra processes. Note that there are quite a few processes running in a normal Erlang emulator, so make sure that you check what processes are running before you try out your code.

Once you have your code working pretty well, try to generate 10K or even 100K prime numbers. (My code takes approximately a minute to generate 100K primes; maybe you can do better!) You don't need to worry about getting a huge output from your program, because the Erlang shell will only print out a small number of list-elements before stopping.

But, it would be cool to actually see 100 or 200 or 500 prime numbers, so add one more function to your proc_sieve module, called gen_print(MaxN). This function's operation will be very simple:

Generate all primes up to MaxN using your generate() function, and then use lists:foreach/2 to map a fun to every number in the list. The fun should take a single argument, an integer, and print out that value on its own line. You can use io:format/2 to do the actual printing. (Hint: You would use the ~w control-sequence to include an integer in formatted output.)

Try out your new gen_print function with 200 or 500 primes, and make sure your results are correct!

All Done!

Once you have completed all of the above work, go ahead and submit your lab on csman.