
For the next three labs we will write a program to render the very well-known Mandelbrot set using a less well-known, and very computationally intensive, approach. Along the way, you will get to explore a number of useful C++ language features, and tools used by many C/C++ programs.
The Mandelbrot set is one of the most well-known fractals; virtually everyone recognizes its iconic shape:

The Mandelbrot set is generated by iterating a specific function zn+1 = zn2 + c, where all values are complex numbers.
Initially, z0 = 0 + 0i. The point c is taken somewhere from the region (-2 - 1.5i) to (1 + 1.5i). The above operation is iterated until the series either diverges, or if it remains bounded. This is approximated by the following conditions:
If |zn| > 2 then the series will diverge, and c is not in the Mandelbrot set. The iterated calculation is terminated once this condition is encountered, since every subsequent iteration will also have this characteristic.
If the above operation is iterated up to some iteration limit, without |zn| > 2, then it is assumed that the series will converge, and c is in the Mandelbrot set.
Of course, this is an approximation. With large enough compute power, and high enough precision in your arithmetic, you can explore the endless detail in the Mandelbrot set. But, this approximation is certainly fine enough to draw pictures like the one above. In that picture, all black pixels are part of the Mandelbrot set. All colored pixels are not part of the Mandelbrot set, and the pixels are colored based on how many iterations were necessary before the |zn| > 2 condition was encountered.
If you have 20 minutes to spare, check out this great Veritasium video about the Mandelbrot set, another remarkable mathematical phenomenon called the logistic map, and many physical processes.
The Mandelbrot set is very fun to explore just using the above simple rendering technique, but there are numerous other ways to render and explore this fascinating mathematical construct. One of the more interesting and compute-intensive approaches is called Buddhabrot, which works like this:
c = a random point in the region (-2 - 1.5i) to (1 + 1.5i)
Use the above iterated function to see if c is in the Mandelbrot set or not. Record all zi for i > 0. (We don't record z0 because z0 = 0 always, and that's boring.)
If c is not in the Mandelbrot set (i.e. the function diverges), then plot all zi (i > 0) in the image as follows: Find the pixel that each zi falls into, and increment its value by 1.
This process is repeated many many times, for many random starting points. (One million random starting locations is at the low end of what is required.) Once this has been completed, the image is normalized, and the result looks something like this:
In other words, for points c that escape (and are therefore not in the Mandelbrot set), we record the entire escape trajectory, and then we use these points to draw a density map.
For this assignment you will start creating a Buddhabrot renderer called bbrot that is able to generate pictures like the above. We are going to create this as a command-line tool that takes its parameters from the command line, and generates its result to standard output. Errors and progress information will be generated to standard error. For example, the above image was generated with an invocation like this:
./bbrot 600 50000000 5000 > image.pgmYou can see that if errors or progress information were output to standard output, that would mess up the image data.
The arguments are as follows:
The first argument is the size of the image to create. The above invocation creates a 600x600 image.
The second argument is the number of random points to generate. The above invocation generates 50,000,000 starting points. (Recall that only the points that escape will be used to update the image.)
The third argument is the maximum number of iterations to try before declaring that a point c is within the Mandelbrot set. The above invocation tries applying the zn+1 = zn2 + c function 5000 times; if the function never exceeds |zi| > 2 over this many times, the point c is considered to be inside the Mandelbrot set. (And, therefore, its trajectory won't be used to update the image.)
The following sections will describe how to implement the various parts of this program. Note that we are providing some initial files to help constrain the architecture of your solution, so that it's easier to extend the program over the next few assignments.
A C++ header file mbrot.h is being provided for you this week, to guide your implementation. In a file mbrot.cpp, you will need to provide an implementation of the compute_mandelbrot() function that operates as described above. Here are some more details.
The compute_mandelbrot() function takes the point c as an argument, and then iterates the Mandelbrot computation up to a maximum of maxiters_ times. The inputs and results of the calculation are stored into a MandelbrotPointInfo struct, which your implementation must return. (Note that this struct is not heap-allocated; you are not returning a pointer to the struct. Because of modern's C++ move operations and copy elision, it is not expensive to return a struct like this.)
These details will be unsurprising, but just to be very specific:
The info-struct's max_iters will be set to the same value as passed to the function.
The info-struct's escaped value should be set to true only if the input point c escapes within max_iters of iterated calculations. Otherwise, it should be false to indicate that c is within the Mandelbrot set.
The info-struct's num_iters value should be the number of iterations your function performed. It should be no more than the max_iters value, and it will almost certainly be much less than max_iters if the point escapes.
If the caller of the function passes true for collect_points, your implementation should store the zi values for i > 0. If collect_points is false then don't store the intermediate points.
Never store z0, since z0 is always 0, and this is uninteresting. The consequence of this is that if collect_points is true, the info-struct's points_in_path member will always have a size equal to the returned num_iters value.
Once you have the Mandelbrot calculation implemented, it's time to build the Buddhabrot rendering program around this engine.
The rest of your work for this week will go into a file bbrot.cpp. Specifically, you will put your main() implementation into this file, along with a number of important helper functions. Again, declarations of these functions are provided in the file bbrot.h. (You will need to add various #include statements to bbrot.h to get it working.)
You have undoubtedly seen many C/C++ programs with this function:
int main(int argc, char **argv)When you invoke your function, argc is the number of entries in the array argv. The first value, argv[0], is always set to the name used to invoke your program, and the remaining values in argv are the arguments passed to the program. For example, with the above invocation, argc = 4, and argv is {"./bbrot", "600", "50000000", "5000", NULL}. (Note that argv[argc] = NULL; this is set up by the OS when your program starts.)
You will need to convert these arguments to integer values. For now, you can use the atoi() function to convert strings to numbers. This means your program won't catch invalid inputs, but we will fix that limitation in a future assignment.
Your program should parse the following arguments:
Image size in pixels. (The image is always square, so you only need one argument for this.)
Total number of random starting points to generate.
Maximum iteration limit for testing a point c for membership in the Mandelbrot set.
All of these values can be of type int.
If the program doesn't get the correct number of arguments, report an error to cerr, and return an exit code of 1. (In other words, main() should return 1 in this situation.) Most importantly, don't crash!
Correspondingly, if your program runs successfully, return an exit code of 0.
Besides parsing arguments, your main() function can also implement the main loop of the Buddhabrot calculation:
Generate a random complex number c in the range (-2 - 1.5i) to (1 + 1.5i)
Call your compute_mandelbrot() function on the value c, with the maximum iteration limit specified by the user. Collect the points that the iterated function generates along the way.
If the point c escapes, update the output image by incrementing every pixel that c's escape-path touches. (If the point c doesn't escape, do nothing.)
Repeat this sequence of steps as many times as the user requested.
You will need a class to represent an image with one value per pixel. Since this is a boring thing to implement, an Image class is provided to you in the file image.h. (You should not need to make any changes to this file.) You can initialize an image of whatever size is needed.
As your program computes, it should output something to tell the user that it is making progress. To this end, your main loop should output a "." (period) after every 100,000 points. You can do this easily if you have a loop variable e.g. i, and output a dot if i % 100000 == 0.
This progress output should go to standard error, not standard output, so that you don't mess up the image data your program will output.
We will make this output much more sophisticated in a future lab.
The C Standard Library has provided a number of random number generators over the years: rand(), random(), drand48(), and so forth. These generators have various limitations, and the use of some are even discouraged. (The man page for rand() even has this title: "rand, rand_r, srand, sranddev -- bad random number generator".) The C++ Standard Library finally addressed this issue in C++11, providing a set of abstractions for implementing sources of pseudo-randomness and true randomness, and also for generating random values with different distributions. It is finally useful for doing scientific and mathematical computing.
All of this great functionality is provided in the C++ <random> header. You are encouraged to read the documentation about the C++ <random> library so you can learn about all of the great features it contains, but so many features also makes it difficult to figure out what to use in our program. So, we'll make it easy:
Use a std::default_random_engine object as your pseudo-random generator.
Use one std::uniform_real_distribution object to generate the real component of your complex numbers, and initialize it for the range [-2, 1).
Use another std::uniform_real_distribution object to generate the imaginary component of your complex numbers, and initialize it for the range [-1.5, 1.5).
Both of the uniform_real_distribution variables can draw from the same random generator. Neat!
All of these variables should live outside the main loop that generates random complex numbers and does the Mandelbrot calculations, so that you get good random results, and also so that you don't incur the overhead of initializing them every iteration through the loop.
Note: You will notice these ranges [-2, 1] and [-1.5, 1.5] showing up regularly in your implementation. Define C++-style typed constants for these values. Don't use the C-style #define to define typed constants in C++ programs.
Once you have generated a random complex number c, and you've used the compute_mandelbrot() function to determine that it isn't in the Mandelbrot set, you will need to update the image with the point's escape-path. There are two helper functions you will implement to do this.
The normalize(min, max, value) function simply normalizes a value to a 0..1 range. This function is useful in several places in the Buddhabrot calculation, so why not factor it out into a helpful tool.
Basically, if value == min, the function should return 0. If value == max, the function should return 1. If value is halfway between min and max, it should return 0.5.
You don't have to do anything special if value < min or value > max; for example, it's fine if your function returns a value < 0 or > 1 in these cases.
However, you should assert that max > min in your function; it simply wouldn't make any sense otherwise.
The update_image(image, info) function should update the image with the contents of the info.points_in_path collection. This update is very straightforward.
for each point in info.points_in_path:
if the point is outside of the region (-2 - 1.5i) to (1 + 1.5i):
skip the point
otherwise:
x = map the real component from [-2, 1] to an integer [0, image_size - 1]
y = map the imaginary component from [-1.5, 1.5] to an integer [0, image_size - 1]
increment the value for the pixel (x, y) in the image
# Since the Buddhabrot image is symmetrical across the X-axis,
# we can get extra points "for free" by mirroring the result!
increment the value for the pixel (x, image_size - y - 1) in the imageAs you might guess, the normalize() function can be very useful in doing the above computations.
You might think that outputting an image from a program is complicated, but there is a family of simple image formats named Netpbm that makes this task very easy. In particular, Netpbm includes several ASCII plaintext image formats, for color images, grayscale images, and bitmap images. ASCII plaintext images are huge, but they are also easy for a program to output, most OSes support them, and you can always convert them into a better format like PNG or JPEG using simple command-line tools.
Since our Buddhabrot rendering technique generates monochrome grayscale images, we will use the Portable GrayMap (PGM) format. The image is an ASCII text file, as follows:
P2 width height max_value
v1 v2 v3 ......and that's it! The P2 value is a "magic number" indicating the grayscale image format. The width, height and maxvalue_ values are all integers; maxvalue_ is simply the largest pixel value in the image, and must be less than 65536. After that, the vi values are simply the grayscale values for the pixels in the image.
(If you ever want to output an RGB image easily, you can use the
P3magic number, and then the only change is that you output 3 values per pixel, instead of just one value per pixel. This is the Portable PixMap format.)
The Netpbm format specifies that no line in the output image should be longer than 70 characters, but you can safely ignore this constraint. Just make sure to emit a newline after the max_value, and also after every row of the image is output. This will help with debugging your program.
In bbrot.cpp you will need to implement the output_image_to_pgm() function to encode the generated image data in ASCII PGM format, and write it out to the specified output-stream. The function needs to work as follows:
1) Find the maximum pixel value in the entire image. In all likelihood, this value will be much larger than 65536.
2) Output the image data in the format above, using a "maximum value" of 255. This means you will need to scale each pixel's value to the range [0..255], using the maximum value you found in step 1 to scale the values appropriately. (You may again find the normalize() function to be very helpful in this calculation.)
As stated before, make sure to emit a newline after the first line with the
magic number and image dimensions, and emit a newline after each line of
image data.
Make sure you only output integer values; ASCII Netpbm doesn't understand
floating-point values.
Finally, make sure that all values are separated with whitespace; failure to
do this can lead to very confusing errors.Make sure to document your code, focusing specifically on writing a reasonably detailed header comment for every function you implemented this week. Use the Doxygen commenting format. (You don't have to provide a Doxyfile or anything like that, unless you really want to.)
As usual, create a Makefile for your project that builds a bbrot binary. Your Makefile should include an all target and a clean target, as usual.
Once you have completed the above steps, it's time to start testing and debugging your program. While all tasks are straightforward, it's easy to be tripped up by the vagaries of C++ floating-point and integer math, and other irritating issues you might encounter. You should stick with low-resolution outputs until you have gotten everything working properly. Then, if you want, you can crank up the settings!
This kind of program will greatly benefit from turning on compiler optimizations, either the -O2 or -O3 setting. If you do this, you will notice a significant performance improvement. Just be aware that this will hinder debugging your program, so you may not want to try this until your code is working well.
Here are some example outputs for you to compare against:
./bbrot 200 1000000 100 > img_100.pgm
./bbrot 200 1000000 500 > img_500.pgm
./bbrot 200 1000000 1000 > img_1000.pgm
You will notice that as you increase the iteration limit, more and more detail will appear in the Buddhabrot output. Also, as you increase the total number of points generated, the image will become less noisy as more detail is filled in. However, it's very easy to sink a lot of time into generating results, so you may want to avoid being too ambitious in your computations.
As a simple example, here is another version of the first image above, with 10M points instead of 1M points:
./bbrot 200 10000000 100 > img_100.pgm
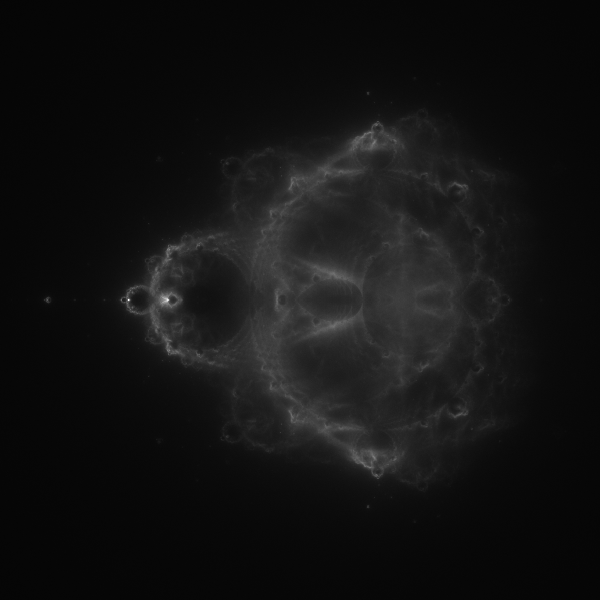
Finally, if you accidentally use the points that don't escape, your plot will look more like this, showing the many lobes of the Mandelbrot set:
Once you have finished testing and debugging your program, submit these files to codePost.io:
mbrot.h and mbrot.cppbbrot.h and bbrot.cppMakefileWe will use a fresh copy of image.h, so you don't need to submit this file.